C Program To Find Second Largest Number
Consider the players A, B, C, D. Have matches between A & B, C & D. Have matches between the winners of match between A & B and C & D. Continue until only two players remain. Have a match between them. The winner is the best player and the loser is the next to best player.
However, before starting on an algorithm based on this method, let us look closely. We will conduct an experiment.
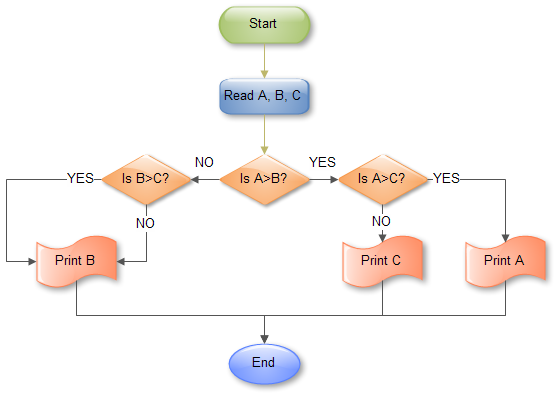
All the element of an array is unique. So there is no repetition. To find second highest element in array whose element is repeated, check for the program to find the.
Find The Second Largest Number
Consider players A, B, C, D, E, E, F, G and H. We will associate with each player a winning capacity number. If two players play a match, the one with a higher number should win (these numbers are just for illustration). Consider A=2, B=3, C=8, D=9, E=6, F=7, G=5 and H=4. Now D and C should be the best and the second-best players since they have the highest numbers. The tournament goes like this: As you can see first prize is correctly awared but for the second prize, F (with number 7) wins rather than C (with number 8).
So you see that this algorithm can fail while finding the second largest. Now let us try to modify the algorithm so that this does not happen. First, why did this happen? This happened because two players with nearly same capacity are placed nearby in the tree.
So, 8 gets defeated by 9 early in the tree. The problem with the algorithm is that, ANY player defeated by the best player can be the second-best, not always the one who lasts till the end. So, after getting the best player, we must carry out another tournament between the players defeated directly by the best to find the second-best player. The first person to have thought of the fact that the second prize is awarded unfairly in tennis tournaments was Lewis Carroll, of Alice in Wonderland fame. After his intervention, a system of seeding was introduced, which helps in placing players with similar capacity further away in the tree. This minimizes the chances of the wrong person getting the second prize.
Even so, the system can err, although the chances are remote. However, our program must be foolproof, so will carry out the extra tournament between the direct losers. From the above tree, the players who have been defeated by D(9) are C(8), B(3) and F(7). So we carry out another tournament: As you can see, C(8) wins. Now we will implement this algorithm.
However, before reading on, take a set of numbers and carry out the two tournaments to get a feel of the algorithm. One implementation problem is that in the first tournament, we must keep track of the players whom the eventual winner is defeating. However, since we don't know who the eventual winner will be, we must keep track of the players getting defeated by all the winners (who have not yet lost). The implementation is shown below.

Int first = arr0; int second = arr0; int i; for(i=0;i. Your code requires approx. 2n comparisons. If you implemented the following method you can do it in approx n+log n comparisons. Organize a 'elimination style tournament' between the numbers. For example you have 4 numbers, Greatest / W1 W2 / / X X X X Where the X's are your numbers, then you require n-1 comparisons to find the greatest.
Then the second greatest could have only been beaten by the greatest number. So it is one of the log n numbers that greatest has beaten. Therefore you need log n comparisons to find second greatest, overall, approx n+log n instead of approx 2n.